圆锥面积公式推导过程(计算最体验,圆锥曲线的面积问题)
日期:2024-08-16 12:15:15 浏览: 100

其实,说到三角形的面积,在解析几何里算是非常重要的了。
因为,毕竟高考卷中,解析几何的困难,有很大一部分都是由它引起的。
当然,它的难处,主要还是体现在计算过程的艰难上。
说到面积,首当其冲,便 是要弄清楚面积的相关公式了。

前面两个公式,是很多时候常用、也是为大家所熟知的。
最后一个公式,虽然很多人可能并不熟悉,但有一个解几里的常用公式,相信你一定是熟悉的。
那就是,当三角形的一个顶点是原点时:
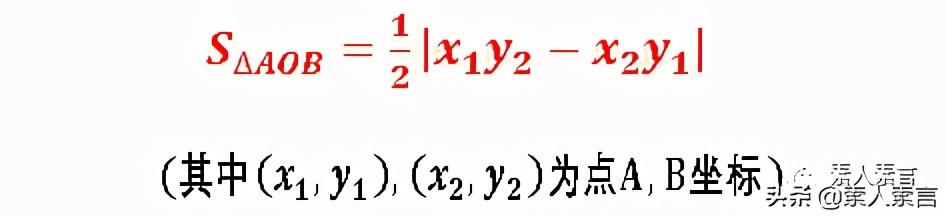
其实,这个结论,可以很容易的用最后一个公式推导验证的。
别不在意,在考试时它的出镜率,可是很高的哦!
三角形的面积公式不多,思路也会很清楚。但在解题时,所需要的计算量却是很大的。
而且,最后基本上都会与函数、不等式进行综合。而不等式,不正是很多孩子心中的恶梦么?
这也是解几难题,大部分都与面积有关的一个重要原因。
其实,能做却做不对的状态,也是最痛苦的了吧。



其实这题,着实是不容易的。
偏偏思路又很清楚。
只是中间的计算量,是不是吓到初学解几的你了呢?
确实还是有些考验人的。
另外,曲线的切线方程,你确定是会的、并且很熟练的么?
不过这些,对我来说,都是小菜了。因为善于观察,在解题的过程中,倒是发现了抛物线的一个很好的结论了。
你发现了吗……



说真的,这个题的计算,应该算得上非常麻烦了。
但你要是仔细揣摩下,题目思维上的难度,又确实是非常低的。
所以说,三角形的面积问题,很多的时候,还是要看计算思路的整理。
只要认准了计算的可能性和方向,
干就完了!
另外,特别要提醒的是,在这里我是非常耿直的用了面积的坐标公式。在正规考试时,可能还是要稍微迂回一点,避免直接写出这个公式,走一个正常化的形式。
也免得让老师尴尬不是?



因为三角形的顶点有一个是原点,所以原本也是想小秀一下坐标公式的。
但从图形中看,直接分割得更方便些,所以便采用了图形分割的方法。
其实,割补法求面积,在解几中也是很常见的事情了。
当然,最后的求最值,虽然因为式子的简洁,还算是顺利,但在实际操作时,相信仍会有不少同学会出问题的。
所以,对于基本不等式的结构、使用条件,务必还是要熟练、再熟练的。

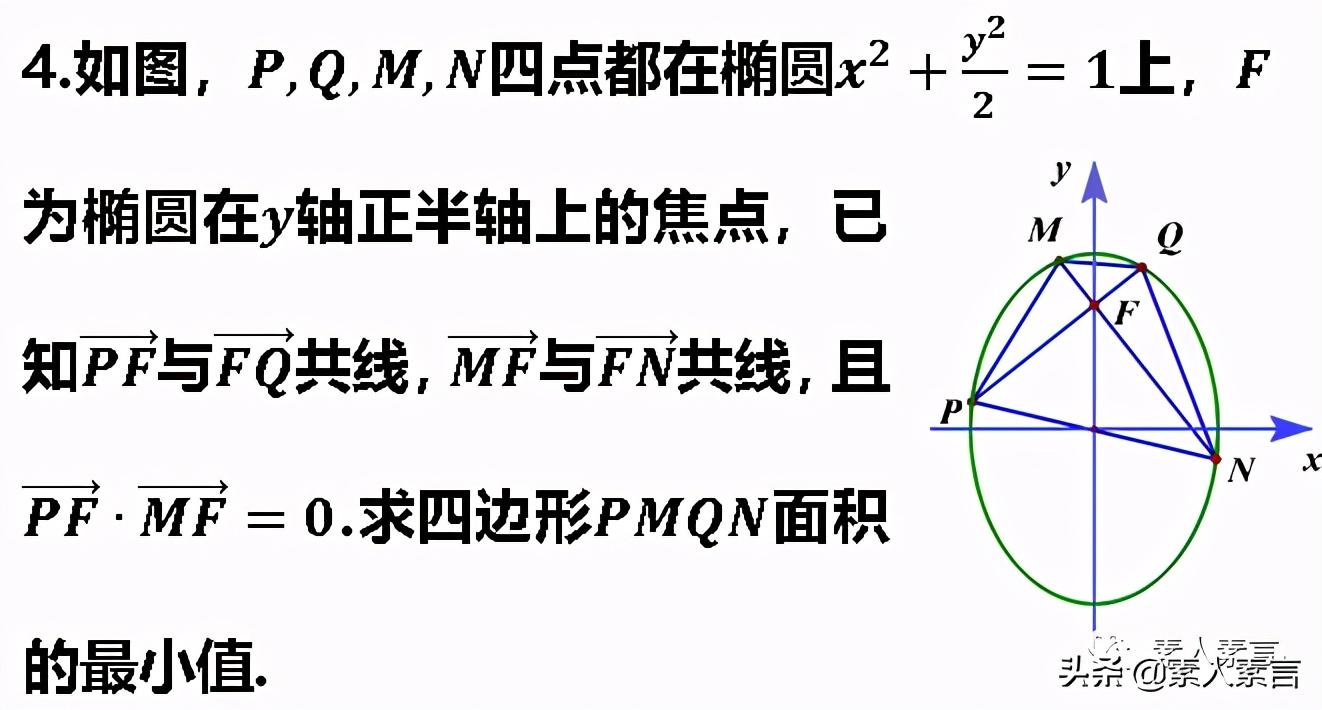

嗯,毫无意外,没有惊喜。
除了计算量,别的也真的没什么。
哦,对了,和前面一样,这里用了两个常用公式,还是要交待一下的。
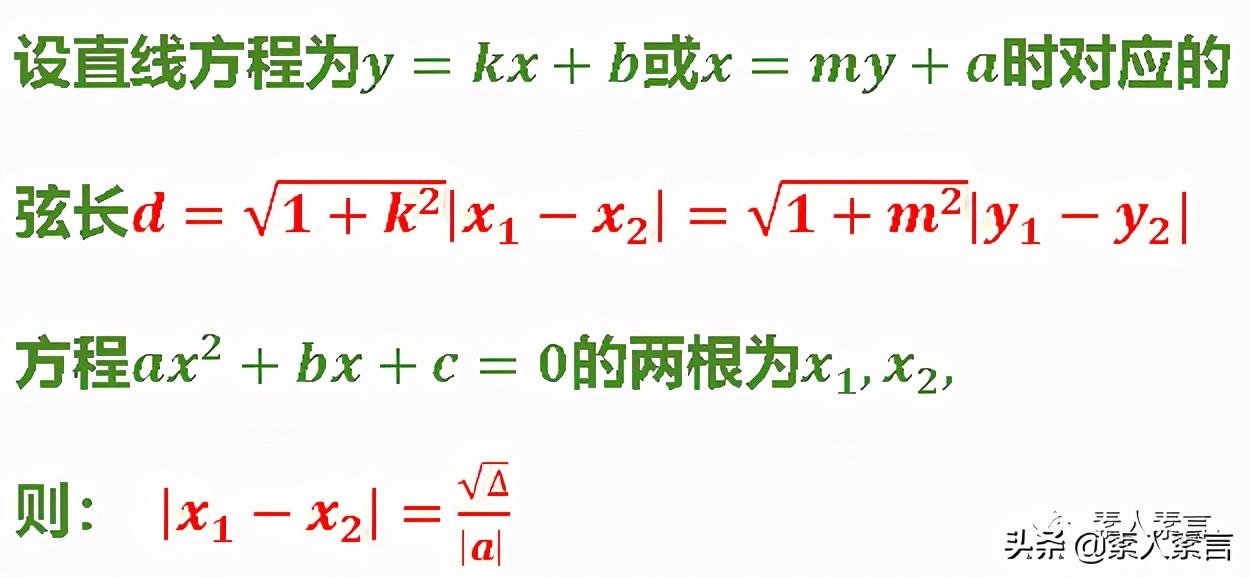
另外,这里还用了一个四边形的面积公式:

当然,对于一个参数方程爱好者来说,一定还是要试试下面这种解法的。

确实,一如以往的,
参数方程总会带给我们莫名的惊喜!

说点感想吧。
解析几何的最值问题,往往综合性强,可能字母或变量也会比较多,往往还会涉及到函数或不等式的相关内容,很多时候,后面的式子一定还会是一个让人生厌的分式。
所以,一直也是高考的热点话题之一。
这里最值问题的处理,往往通过代数法,通过构造函数并利用函数的最值求出其最值。
所以,主要还是对计算能力和代数的要求较高了。




















