浮点型是什么(浮点数在计算机内的表示)
日期:2024-08-15 10:00:21 浏览: 100
浮点数的表示
小数点的位置可以在数据位之间移动的数据称为浮点型数据,与数学中的实数相对应,与定点数相比,它的表示范围可以更大,还存在一个数据精度(有效数字位数)的问题。
例如:123.456可用如下多种表示:
12.3456×101
0.123456×103
1.23456×102,只有最后这种表示属于科学计数法 计算机中浮点数据编码的一般形式为: N=(-1)S×M×RE
在计算机中,浮点数通常被表示成如下格式:

其中:S:代表符号位,0代表正,1代表负,是浮点数(即尾数部分)的符号。 M:代表尾数,也就是有效数字,用定点小数表示,通常用原码表示。
R:指数的底,约定为2,不必表示出来,E:代表阶码,是一个整数,可正可负,一般用移码表示,用RE×尾数M可得到浮点数的绝对值。
合理地选择阶码和尾数的位数m和n的值是十分重要的,以便在总长度为1+m+n位二进制表示的浮点数中,既保证有足够大的数值范围(取决于m),又保证有所要求的数值精度(取决于n)。
需要对浮点数的表示和运算做出某些规定,国际上得到普遍应用的是IEEE-754标准,明确规定了表示浮点数所用的位数和几个字段的分配关系,规格化表示和规格化操作,隐藏位的使用等方案,如表2.4所示:
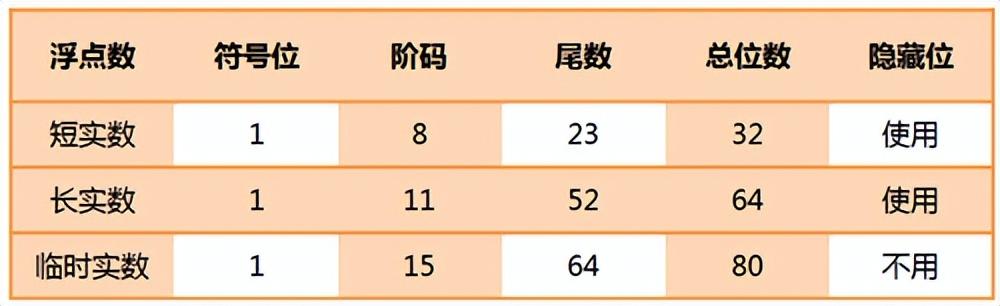
表2.4 三种浮点数格式
请注意,1位的符号位用于表示浮点数的符号,也可以说是尾数的符号。
32位或64位的尾数用于表示数值,规定用规格化的原码小数表示。
规格化
规格化是指非0值的浮点数的位数必须满足1/2≤|M|<1的要求,即小数点后的最高位数字必须为1。在遇到不满足这一规定的情况下,需要把非规格化的浮点数变成为规格化表示的浮点数,这项操作被称为规格化操作。使用规格化的浮点数便于浮点数之间的运算与比较,也有利于提高浮点数的表示精度。
既然尾数的最高位的值一定要为1,在实用中,可以通过把整个尾数左移一位的办法把最高位的这个1移走,使受尾数位数限制不能被保存的更低一位上的一个数位得以保存,从而提高了一个二进制位的表示精度,这项处理方案被称为隐藏位技术,被用于单精度和双精度浮点数的存储中。临时浮点数中不使用隐藏位技术。
8位或11位的阶码用作为以2为底的一个指数的幂,只能是整数,它的位数决定了浮点数的表示范围,通常用移码表示,移码由1位符号位和n位数据位构成。
对于一个n+1位的整数,移码的定义是 [x]移=2n + x,其表示范围-2n≤x <2n,例如,8位的移码是27+ X,称为移128的方案,移码形式的机器数比数X在数轴上右移了128。
X=-127,[x]移=27+X=128 +(-127) = 1 =(00000001)2 ,
X= 127,[x]移=27+X=128 + 127 = 255 =(11111111)2
请注意,移码只用于表示整数,仅用在浮点数的阶码部分。对同一个X,其移码数与补码数有简单的对应关系,数值位相同,符号位相反,移码用0表示负号,1表示正号。
使用移码的优点是:便于比较两个移码数的大小,移码表示的机器数与数在数轴上的排列关系一致,正数大于负数,用在浮点数的阶码部分时,有利于加快浮点数的比较的速度,有利于判断浮点数的0。




















